DOMÍNIO, CONTRADOMÍNIO E IMAGEM DE UMA FUNÇÃO
Função x
2, definida para { -3,-2,-1,0 }. Observar o conjunto domínio (D),
contradomínio (CD) e imagem (delineado pela linha tracejada).
Considere dois
conjuntos X e
Y. Uma função
f de
X em
Y:

relaciona com cada elemento
x em
X, um único elemento
y=
f(
x) em
Y.
- f é unívoca: se y = f(x) e z = f(x), então y = z.
- f é total: para todos x em X, existe um y em Y tal que y = f(x).
Se a segunda condição é atendida, mas a primeira não, temos uma
função multivalorada, o termo função multívoca é, por vezes utilizado na mesma acepção.
Se a primeira condição é atendida, mas a segunda não, temos uma
função parcial.
Considere as três funções seguintes:
 | Esta não é uma função, pois o elemento 3 em X é associado com dois elementos (d e c) em Y (a correspondência é funcional). Apesar de não ser uma função, representa uma função multivalorada. |
 | Esta não é uma função, pois o elemento 1 em X não é associado com um elemento em Y. Apesar de não ser uma função, representa uma função parcial. |
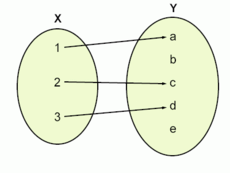 |
-
-
- Esta é uma função (no caso, uma função discreta). Ela pode ser definida explicitamente pela expressão:
-
 -
-
-
-
-
-
-
|

















